Giải phương trình $4^x + 6^x = 9^x$

Bài này chủ yếu để luyện lại LOGARIT (kiến thức lớp 12). Hướng đi của mình là các bạn đưa về giải phương trình bậc 2 rồi dùng Logarit để tìm nghiệm.

Đề bài: Giải phương trình

$4^x+6^x=9^x$

Để đưa về phương trình bậc 2, trước tiên các bạn chia cả 2 vế cho $9^x$

Phương trình: $\frac{4^x+6^x}{9^x} = 1$

$\Leftrightarrow \frac{4^x}{9^x} + \frac{6^x}{9^x }=1$

$\Leftrightarrow (\frac{4}{9})^x + (\frac{6}{9})^x = 1$

$\Leftrightarrow (\frac{2}{3})^{2x} + (\frac{2}{3})^x - 1 = 0$

Đặt $\frac{2}{3}^x = t$ (Điều kiện: $t>0$)

Phương trình: $\Leftrightarrow t^2+t-1=0$

Sau khi giải phương trình bậc 2, các bạn được 2 nghiệm của t là: $t_1=\frac{-1+\sqrt{5}}{2}$, $t_2=\frac{-1-\sqrt{5}}{2}$ (loại $t2$ vì $t>0$)

Ở đây, các bạn chỉ cần áp dụng Logarit là có thể tìm được nghiệm: $a^x=b \Rightarrow x={log_{a}}^{b}$

Cũng vậy

 $(\frac{2}{3})^x=\frac{-1+\sqrt{5}}{2}$ 

$\Leftrightarrow x={log_{\frac{2}{3}}}^{\frac{-1+\sqrt{5}}{2}} \approx 1,187$

Hoặc sử dụng đồ thị các bạn cũng có thể thấy đồ thị cắt nhau tại 1 điểm $x_0 > 1$

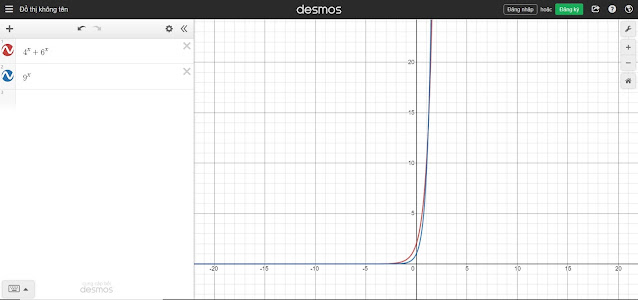Vẽ đồ thị online

Cảm ơn các bạn đã dành thời gian để xem Blog !