Bài toán nghiệm đối xứng $x^2=17x+y$
Hôm nay mình sẽ mang đến cho các bạn một bài toán khá hay, chúng ta thường hay bắt gặp những bài toán đối xứng như vậy trong kì thi học sinh giỏi hay những bài toán ăn điểm trong các đề kiểm tra. Giờ chúng ta cùng bắt đầu tìm hiểu nhé!!!
(Nguồn: Youtube Channel: MindYourDecisions). (Thanks Alslah from India)
Đề bài như sau:
Giả sử
$x^{2}=17x+y$$y^{2}=x+17y$
Với $x\neq y$
Tính $\sqrt{x^{2}+y^{2}+1}=?$
Hãy đặt bút xuống và bắt đầu giải quyết bài toán này nào...
Đối với bài toán này, mình sẽ giải quyết theo 2 hướng nha. Hướng thứ nhất là tự luận, trình bày theo logic để tiếp cận bài toán và hướng thứ hai là chúng ta sử dụng máy tính Casio để giải quyết.
Cách 1:
Chú ý rằng, nếu chúng ta cộng 2 vế của 2 phương trình đề bài cho, như sau:
$x^{2}=17x+y$
$+(y^{2}=x+17y)$
$\rightarrow x^2+y^2 = 18x+18y = 18(x+y)$ $(1)$
Giờ, chúng ta chỉ cần tính $x+y$ là sẽ tìm được kết quả bài toán, để tính x+y, chúng ta trừ 2 vế của 2 phương cho nhau:
$x^2=17x+y$
$-(y^2=x+17y)$
$\rightarrow x^2-y^2 = 16x-16y = 16(x-y)$
$\rightarrow (x-y)(x+y)=16(x-y)$
Vì $x \neq y$ nên $x-y \neq 0$
Do đó, chia 2 vế cho $x-y$, ta được: $x+y$=16
Thay vào $(1)$, ta được: $x^2+y^2=18.16$.
*Tới đây các bạn chỉ việc bấm máy tính là có thể ăn điểm trọn vẹn của câu này, hoặc để hay hơn một chút nữa thì các bạn chú ý $+1$ trong yêu cầu của đề bài $\sqrt{x^{2}+y^{2}+1}$.
Để khử $+1$, các bạn đưa về: $x^2+y^2=(17+1)(17-1)=17^2-1^2=17^2-1$
Vậy $\sqrt{x^{2}+y^{2}+1}$ = $\sqrt{17^2-1+1}$=17
Cách 2:
Phương pháp này không được hay lắm, nhưng nếu những bạn chưa làm quen với những dạng toán như vậy, hoặc trong phòng thi chúng ta nhất thời không nghĩ ra hướng giải quyết hay với xu hướng thi trắc nghiệm như hiện nay. Thì chúng ta hoàn toàn có thể giải bài toán này bằng cách sử dụng máy tính Casio để tìm nghiệm thủ công.
Trước tiên, với 2 phương trình mà đề bài cho, chúng ta hãy đưa chúng về một phương trình 1 ẩn.
$x^2=17x+y \Rightarrow y = x^2-17x$
Thay vào phương trình thứ 2, ta được
$(x^2-17x)^2=x+17(x^2-17x)$
- Đến đây, các bạn có thể dùng hằng đẳng thức rồi đưa về giải phương trình bậc 3
$x^4-34x^3+289x^2=x+17x^2-289x$ $(1)$
Nếu $x=0 \rightarrow y = 0$, mà $x \neq y$ nên $x,y \neq 0$
Do đó, chia 2 vế của $(1)$ cho x, ta được
$x^3-34x^2+272x+288=0$
Các bạn giải phương trình và được 3 nghiệm của x rồi thế vào y và ra được kết quả.
- Hoặc chúng ta sẽ giải nhanh bằng máy tính bỏ túi Casio
$(x^2-17x)^2=x+17(x^2-17x)$
Biết $x \neq 0$ nên chia 2 vế cho $x$ để loại nghiệm 0 và nhập vào máy Casio
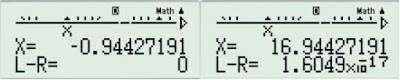
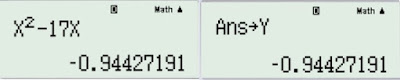
Tiếp tục nhấn $Shift \rightarrow SOLVE \rightarrow =$, bạn sẽ tìm được $x$ là một trong 2 nghiệm sauBạn thay vào $y=x^2-17x$, vì $x,y$ đối xứng nên 2 giá trị trên chính là của x và yKhi bạn giải ra nghiệm, máy tính sẽ tự lưu vào biến $X$, ví dụ mình chọn $x=16,94427191$. Tính $y$ rồi nhấn $Shift \rightarrow STO \rightarrow Y$ để lưu kết quả vào biến $Y$
Giờ các bạn nhập $X$ và $Y$ theo yêu cầu đề bài là ra kết quả
Cảm ơn các bạn đã theo dõi Blog, nếu thấy bài viết hữu ích hay ấn like và để lại một bình luận để ủng hộ mình nhé !!!





Nhận xét từ Facebook